Question 1.
Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In figure, if AB – PQ and PQ = XY, then AB = XY.
Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In figure, if AB – PQ and PQ = XY, then AB = XY.
Solution:
(i) False
Reason : If we mark a point O on the surface of a paper. Using pencil and scale, we can draw infinite number of straight lines passing
through O.
(ii) False
Reason : In the following figure, there are many straight lines passing through P. There are many lines, passing through Q. But there is one and only one line which is passing through P as well as Q.
(iii) True
Reason: The postulate 2 says that “A terminated line can be produced indefinitely.”
(iv) True
Reason : Superimposing the region of one circle on the other, we find them coinciding. So, their centres and boundaries coincide.
Thus, their radii will coincide or equal.
(v) True
Reason : According to Euclid’s axiom, things which are equal to the same thing are equal to one another.
Question 2.
Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them?
(i) Parallel lines
(ii) Perpendicular lines
(iii) Line segment
(iv) Radius of a circle
(v) Square
(i) False
Reason : If we mark a point O on the surface of a paper. Using pencil and scale, we can draw infinite number of straight lines passing
through O.
(ii) False
Reason : In the following figure, there are many straight lines passing through P. There are many lines, passing through Q. But there is one and only one line which is passing through P as well as Q.
(iii) True
Reason: The postulate 2 says that “A terminated line can be produced indefinitely.”
(iv) True
Reason : Superimposing the region of one circle on the other, we find them coinciding. So, their centres and boundaries coincide.
Thus, their radii will coincide or equal.
(v) True
Reason : According to Euclid’s axiom, things which are equal to the same thing are equal to one another.
Question 2.
Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them?
(i) Parallel lines
(ii) Perpendicular lines
(iii) Line segment
(iv) Radius of a circle
(v) Square
Solution:
Yes, we need to have an idea about the terms like point, line, ray, angle, plane, circle and quadrilateral, etc. before defining the required terms.
Definitions of the required terms are given below:
(i) Parallel Lines:
Two lines l and m in a plane are said to be parallel, if they have no common point and we write them as l ॥ m.
(ii) Perpendicular Lines:
Two lines p and q lying in the same plane are said to be perpendicular if they form a right angle and we write them as p ⊥ q.
(iii) Line Segment:
A line segment is a part of line and having a definite length. It has two end-points. In the figure, a line segment is shown having end points A and B. It is written as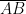
or
.
(iv) Radius of a circle :
The distance from the centre to a point on the circle is called the radius of the circle. In the figure, P is centre and Q is a point on the circle, then PQ is the radius.
(v) Square :
A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a square. Given figure, PQRS is a square.
Question 3.
Consider two ‘postulates’ given below
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist atleast three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
Definitions of the required terms are given below:
(i) Parallel Lines:
Two lines l and m in a plane are said to be parallel, if they have no common point and we write them as l ॥ m.
(ii) Perpendicular Lines:
Two lines p and q lying in the same plane are said to be perpendicular if they form a right angle and we write them as p ⊥ q.
(iii) Line Segment:
A line segment is a part of line and having a definite length. It has two end-points. In the figure, a line segment is shown having end points A and B. It is written as
or
.
(iv) Radius of a circle :
The distance from the centre to a point on the circle is called the radius of the circle. In the figure, P is centre and Q is a point on the circle, then PQ is the radius.
(v) Square :
A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a square. Given figure, PQRS is a square.
Question 3.
Consider two ‘postulates’ given below
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist atleast three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
Solution:
Yes, these postulates contain undefined terms such as ‘Point and Line’. Also, these postulates are consistent because they deal with two different situations as
(i) says that given two points A and B, there is a point C lying on the line in between them. Whereas
(ii) says that, given points A and B, you can take point C not lying on the line through A and B.
No, these postulates do not follow from Euclid’s postulates, however they follow from the axiom, “Given two distinct points, there is a unique line that passes through them.”
Question 4.
If a point C lies between two points A and B such that AC = BC, then prove that AC =
AB, explain by drawing the figure.
(i) says that given two points A and B, there is a point C lying on the line in between them. Whereas
(ii) says that, given points A and B, you can take point C not lying on the line through A and B.
No, these postulates do not follow from Euclid’s postulates, however they follow from the axiom, “Given two distinct points, there is a unique line that passes through them.”
Question 4.
If a point C lies between two points A and B such that AC = BC, then prove that AC =
AB, explain by drawing the figure.
Solution:
We have,
AC = BC [Given]
∴ AC + AC = BC + AC
[If equals added to equals then wholes are equal]
or 2AC = AB [∵ AC + BC = AB]
or AC =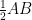
Question 5.
In question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
We have,
AC = BC [Given]
∴ AC + AC = BC + AC
[If equals added to equals then wholes are equal]
or 2AC = AB [∵ AC + BC = AB]
or AC =
Question 5.
In question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Solution:
Let the given line AB is having two mid points ‘C’ and ‘D’.
AC =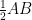
……(i)
and AD =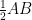
……(ii)
Subtracting (i) from (ii), we have
AD – AC =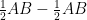
or AD – AC = 0 or CD = 0
∴ C and D coincide.
Thus, every line segment has one and only one mid-point.
Question 6.
In figure, if AC = BD, then prove that AB = CD.
AC =
……(i) and AD =
……(ii) Subtracting (i) from (ii), we have
AD – AC =
or AD – AC = 0 or CD = 0
∴ C and D coincide.
Thus, every line segment has one and only one mid-point.
Question 6.
In figure, if AC = BD, then prove that AB = CD.
Solution:
Given: AC = BD
⇒ AB + BC = BC + CD
Subtracting BC from both sides, we get
AB + BC – BC = BC + CD – BC
[When equals are subtracted from equals, remainders are equal]
⇒ AB = CD
Question 7.
Why is axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that, the question is not about the fifth postulate.)
Given: AC = BD
⇒ AB + BC = BC + CD
Subtracting BC from both sides, we get
AB + BC – BC = BC + CD – BC
[When equals are subtracted from equals, remainders are equal]
⇒ AB = CD
Question 7.
Why is axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that, the question is not about the fifth postulate.)
Solution:
As statement is true in all the situations. Hence, it is considered a ‘universal truth.’
Exercise 5.2
Exercise 5.2
Question 1.
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand
Solution:
We can write Euclid’s fifth postulate as ‘Two distinct intersecting lines cannot be parallel to the same line.’
Question 2.
Does Euclid’s fifth postulate imply the existence of parallel lines ? Explain.
We can write Euclid’s fifth postulate as ‘Two distinct intersecting lines cannot be parallel to the same line.’
Question 2.
Does Euclid’s fifth postulate imply the existence of parallel lines ? Explain.
Solution:
Yes. If a straight line l falls on two lines m and n such that sum of the interior angles on one side of l is two right angles, then by Euclid’s fifth postulate, lines m and n will not meet on this side of l. Also, we know that the sum of the interior angles on the other side of the line l will be two right angles too. Thus, they will not meet on the other side also.
∴ The lines m and n never meet, i.e, They are parallel.
Yes. If a straight line l falls on two lines m and n such that sum of the interior angles on one side of l is two right angles, then by Euclid’s fifth postulate, lines m and n will not meet on this side of l. Also, we know that the sum of the interior angles on the other side of the line l will be two right angles too. Thus, they will not meet on the other side also.
∴ The lines m and n never meet, i.e, They are parallel.