Question 1.
In quadrilateral ACBD, AC = AD and AB bisects ∠ A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?
In quadrilateral ACBD, AC = AD and AB bisects ∠ A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?

Solution:
In quadrilateral ACBD, we have AC = AD and AB being the bisector of ∠A.
Now, In ∆ABC and ∆ABD,
AC = AD (Given)
∠ CAB = ∠ DAB ( AB bisects ∠ CAB)
and AB = AB (Common)
∴ ∆ ABC ≅ ∆ABD (By SAS congruence axiom)
∴ BC = BD (By CPCT)
Question 2.
ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA (see figure). Prove that
(i) ∆ABD ≅ ∆BAC
Now, In ∆ABC and ∆ABD,
AC = AD (Given)
∠ CAB = ∠ DAB ( AB bisects ∠ CAB)
and AB = AB (Common)
∴ ∆ ABC ≅ ∆ABD (By SAS congruence axiom)
∴ BC = BD (By CPCT)
Question 2.
ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA (see figure). Prove that

(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠ BAC
(iii) ∠ABD = ∠ BAC
Solution:
In quadrilateral ACBD, we have AD = BC and ∠ DAB = ∠ CBA
(i) In ∆ ABC and ∆ BAC,
AD = BC (Given)
∠DAB = ∠CBA (Given)
AB = AB (Common)
∴ ∆ ABD ≅ ∆BAC (By SAS congruence)
(ii) Since ∆ABD ≅ ∆BAC
⇒ BD = AC [By C.P.C.T.]
(iii) Since ∆ABD ≅ ∆BAC
⇒ ∠ABD = ∠BAC [By C.P.C.T.]
Question 3.
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.
(i) In ∆ ABC and ∆ BAC,
AD = BC (Given)
∠DAB = ∠CBA (Given)
AB = AB (Common)
∴ ∆ ABD ≅ ∆BAC (By SAS congruence)
(ii) Since ∆ABD ≅ ∆BAC
⇒ BD = AC [By C.P.C.T.]
(iii) Since ∆ABD ≅ ∆BAC
⇒ ∠ABD = ∠BAC [By C.P.C.T.]
Question 3.
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

Solution:
In ∆BOC and ∆AOD, we have
∠BOC = ∠AOD
BC = AD [Given]
∠BOC = ∠AOD [Vertically opposite angles]
∴ ∆OBC ≅ ∆OAD [By AAS congruency]
⇒ OB = OA [By C.P.C.T.]
i.e., O is the mid-point of AB.
Thus, CD bisects AB.
Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC = ∆CDA.
∠BOC = ∠AOD
BC = AD [Given]
∠BOC = ∠AOD [Vertically opposite angles]
∴ ∆OBC ≅ ∆OAD [By AAS congruency]
⇒ OB = OA [By C.P.C.T.]
i.e., O is the mid-point of AB.
Thus, CD bisects AB.
Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC = ∆CDA.

Solution:
∵ p || q and AC is a transversal,
∴ ∠BAC = ∠DCA …(1) [Alternate interior angles]
Also l || m and AC is a transversal,
∴ ∠BCA = ∠DAC …(2)
[Alternate interior angles]
Now, in ∆ABC and ∆CDA, we have
∠BAC = ∠DCA [From (1)]
CA = AC [Common]
∠BCA = ∠DAC [From (2)]
∴ ∆ABC ≅ ∆CDA [By ASA congruency]
Question 5.
Line l is the bisector of an ∠ A and ∠ B is any point on l. BP and BQ are perpendiculars from B to the arms of LA (see figure). Show that
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms ot ∠A.
∴ ∠BAC = ∠DCA …(1) [Alternate interior angles]
Also l || m and AC is a transversal,
∴ ∠BCA = ∠DAC …(2)
[Alternate interior angles]
Now, in ∆ABC and ∆CDA, we have
∠BAC = ∠DCA [From (1)]
CA = AC [Common]
∠BCA = ∠DAC [From (2)]
∴ ∆ABC ≅ ∆CDA [By ASA congruency]
Question 5.
Line l is the bisector of an ∠ A and ∠ B is any point on l. BP and BQ are perpendiculars from B to the arms of LA (see figure). Show that
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms ot ∠A.

Solution:
We have, l is the bisector of ∠QAP.
∴ ∠QAB = ∠PAB
∠Q = ∠P [Each 90°]
∠ABQ = ∠ABP
[By angle sum property of A]
Now, in ∆APB and ∆AQB, we have
∠ABP = ∠ABQ [Proved above]
AB = BA [Common]
∠PAB = ∠QAB [Given]
∴ ∆APB ≅ ∆AQB [By ASA congruency]
Since ∆APB ≅ ∆AQB
⇒ BP = BQ [By C.P.C.T.]
i. e., [Perpendicular distance of B from AP]
= [Perpendicular distance of B from AQ]
Thus, the point B is equidistant from the arms of ∠A.
Question 6.
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
We have, l is the bisector of ∠QAP.
∴ ∠QAB = ∠PAB
∠Q = ∠P [Each 90°]
∠ABQ = ∠ABP
[By angle sum property of A]
Now, in ∆APB and ∆AQB, we have
∠ABP = ∠ABQ [Proved above]
AB = BA [Common]
∠PAB = ∠QAB [Given]
∴ ∆APB ≅ ∆AQB [By ASA congruency]
Since ∆APB ≅ ∆AQB
⇒ BP = BQ [By C.P.C.T.]
i. e., [Perpendicular distance of B from AP]
= [Perpendicular distance of B from AQ]
Thus, the point B is equidistant from the arms of ∠A.
Question 6.
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Solution:
We have, ∠BAD = ∠EAC
Adding ∠DAC on both sides, we have
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠DAE
Now, in ∆ABC and ∆ADE. we have
∠BAC = ∠DAE [Proved above]
AB = AD [Given]
AC = AE [Given]
∴ ∆ABC ≅ ∆ADE [By SAS congruency]
⇒ BC = DE [By C.P.C.T.]
Question 7.
AS is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB. (see figure). Show that
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE
Solution:
We have, P is the mid-point of AB.
∴ AP = BP
∠EPA = ∠DPB [Given]
Adding ∠EPD on both sides, we get
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
(i) Now, in ∆DAP and ∆EBP, we have
∠PAD = ∠PBE [ ∵∠BAD = ∠ABE]
AP = BP [Proved above]
∠DPA = ∠EPB [Proved above]
∴ ∆DAP ≅ ∆EBP [By ASA congruency]
(ii) Since, ∆ DAP ≅ ∆ EBP
⇒ AD = BE [By C.P.C.T.]
Question 8.
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = AB
AB
Adding ∠DAC on both sides, we have
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠DAE
Now, in ∆ABC and ∆ADE. we have
∠BAC = ∠DAE [Proved above]
AB = AD [Given]
AC = AE [Given]
∴ ∆ABC ≅ ∆ADE [By SAS congruency]
⇒ BC = DE [By C.P.C.T.]
Question 7.
AS is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB. (see figure). Show that
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE

Solution:
We have, P is the mid-point of AB.
∴ AP = BP
∠EPA = ∠DPB [Given]
Adding ∠EPD on both sides, we get
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
(i) Now, in ∆DAP and ∆EBP, we have
∠PAD = ∠PBE [ ∵∠BAD = ∠ABE]
AP = BP [Proved above]
∠DPA = ∠EPB [Proved above]
∴ ∆DAP ≅ ∆EBP [By ASA congruency]
(ii) Since, ∆ DAP ≅ ∆ EBP
⇒ AD = BE [By C.P.C.T.]
Question 8.
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB

(iv) CM =
Solution:
Since M is the mid – point of AB.
∴ BM = AM
(i) In ∆AMC and ∆BMD, we have
CM = DM [Given]
∠AMC = ∠BMD [Vertically opposite angles]
AM = BM [Proved above]
∴ ∆AMC ≅ ∆BMD [By SAS congruency]
(ii) Since ∆AMC ≅ ∆BMD
⇒ ∠MAC = ∠MBD [By C.P.C.T.]
But they form a pair of alternate interior angles.
∴ AC || DB
Now, BC is a transversal which intersects parallel lines AC and DB,
∴ ∠BCA + ∠DBC = 180° [Co-interior angles]
But ∠BCA = 90° [∆ABC is right angled at C]
∴ 90° + ∠DBC = 180°
⇒ ∠DBC = 90°
(iii) Again, ∆AMC ≅ ∆BMD [Proved above]
∴ AC = BD [By C.P.C.T.]
Now, in ∆DBC and ∆ACB, we have
BD = CA [Proved above]
∠DBC = ∠ACB [Each 90°]
BC = CB [Common]
∴ ∆DBC ≅ ∆ACB [By SAS congruency]
(iv) As ∆DBC ≅ ∆ACB
DC = AB [By C.P.C.T.]
But DM = CM [Given]
∴ CM = DC =
DC =  AB
AB
⇒ CM = AB
AB
0°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2∠BCD +180° = 360° [∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360° – 180° = 180°
⇒ ∠BCD = = 90°
= 90°
Thus, ∠BCD = 90°
Exercise 7.2
∴ BM = AM
(i) In ∆AMC and ∆BMD, we have
CM = DM [Given]
∠AMC = ∠BMD [Vertically opposite angles]
AM = BM [Proved above]
∴ ∆AMC ≅ ∆BMD [By SAS congruency]
(ii) Since ∆AMC ≅ ∆BMD
⇒ ∠MAC = ∠MBD [By C.P.C.T.]
But they form a pair of alternate interior angles.
∴ AC || DB
Now, BC is a transversal which intersects parallel lines AC and DB,
∴ ∠BCA + ∠DBC = 180° [Co-interior angles]
But ∠BCA = 90° [∆ABC is right angled at C]
∴ 90° + ∠DBC = 180°
⇒ ∠DBC = 90°
(iii) Again, ∆AMC ≅ ∆BMD [Proved above]
∴ AC = BD [By C.P.C.T.]
Now, in ∆DBC and ∆ACB, we have
BD = CA [Proved above]
∠DBC = ∠ACB [Each 90°]
BC = CB [Common]
∴ ∆DBC ≅ ∆ACB [By SAS congruency]
(iv) As ∆DBC ≅ ∆ACB
DC = AB [By C.P.C.T.]
But DM = CM [Given]
∴ CM =
⇒ CM =
0°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2∠BCD +180° = 360° [∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360° – 180° = 180°
⇒ ∠BCD =
Thus, ∠BCD = 90°
Exercise 7.2
Question 7.
ABC is a right angled triangle in which ∠A = 90° and AB = AC, find ∠B and ∠C.
ABC is a right angled triangle in which ∠A = 90° and AB = AC, find ∠B and ∠C.
Solution:
In ∆ABC, we have AB = AC [Given]
∴ Their opposite angles are equal.

⇒ ∠ACB = ∠ABC
Now, ∠A + ∠B + ∠C = 180° [Angle sum property of a ∆]
⇒ 90° + ∠B + ∠C = 180° [∠A = 90°(Given)]
⇒ ∠B + ∠C= 180°- 90° = 90°
But ∠B = ∠C
∠B = ∠C =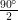 = 45°
= 45°
Thus, ∠B = 45° and ∠C = 45°
Question 8.
Show that the angles of an equilateral triangle are 60° each.
∴ Their opposite angles are equal.

⇒ ∠ACB = ∠ABC
Now, ∠A + ∠B + ∠C = 180° [Angle sum property of a ∆]
⇒ 90° + ∠B + ∠C = 180° [∠A = 90°(Given)]
⇒ ∠B + ∠C= 180°- 90° = 90°
But ∠B = ∠C
∠B = ∠C =
Thus, ∠B = 45° and ∠C = 45°
Question 8.
Show that the angles of an equilateral triangle are 60° each.
Solution:
In ∆ABC, we have

AB = BC = CA
[ABC is an equilateral triangle]
AB = BC
⇒ ∠A = ∠C …(1) [Angles opposite to equal sides of a A are equal]
Similarly, AC = BC
⇒ ∠A = ∠B …(2)
From (1) and (2), we have
∠A = ∠B = ∠C = x (say)
Since, ∠A + ∠B + ∠C = 180° [Angle sum property of a A]
∴ x + x + x = 180o
⇒ 3x = 180°
⇒ x = 60°
∴ ∠A = ∠B = ∠C = 60°
Thus, the angles of an equilateral triangle are 60° each.
Exercise 7.3

AB = BC = CA
[ABC is an equilateral triangle]
AB = BC
⇒ ∠A = ∠C …(1) [Angles opposite to equal sides of a A are equal]
Similarly, AC = BC
⇒ ∠A = ∠B …(2)
From (1) and (2), we have
∠A = ∠B = ∠C = x (say)
Since, ∠A + ∠B + ∠C = 180° [Angle sum property of a A]
∴ x + x + x = 180o
⇒ 3x = 180°
⇒ x = 60°
∴ ∠A = ∠B = ∠C = 60°
Thus, the angles of an equilateral triangle are 60° each.
Exercise 7.3
Question 1.
∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that

(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
Solution:
(i) In ∆ABD and ∆ACD, we have
AB = AC [Given]
AD = DA [Common]
BD = CD [Given]
∴ ∆ABD ≅ ∆ACD [By SSS congruency]
∠BAD = ∠CAD [By C.P.C.T.] …(1)
(ii) In ∆ABP and ∆ACP, we have
AB = AC [Given]
∠BAP = ∠CAP [From (1)]
∴ AP = PA [Common]
∴ ∆ABP ≅ ∆ACP [By SAS congruency]
(iii) Since, ∆ABP ≅ ∆ACP
⇒ ∠BAP = ∠CAP [By C.P.C.T.]
∴ AP is the bisector of ∠A.
Again, in ∆BDP and ∆CDP,
we have BD = CD [Given]
DP = PD [Common]
BP = CP [ ∵ ∆ABP ≅ ∆ACP]
⇒ A BDP = ACDP [By SSS congruency]
∴ ∠BDP = ∠CDP [By C.P.C.T.]
⇒ DP (or AP) is the bisector of ∠BDC
∴ AP is the bisector of ∠A as well as ∠D.
(iv) As, ∆ABP ≅ ∆ACP
⇒ ∠APS = ∠APC, BP = CP [By C.P.C.T.]
But ∠APB + ∠APC = 180° [Linear Pair]
∴ ∠APB = ∠APC = 90°
⇒ AP ⊥ BC, also BP = CP
Hence, AP is the perpendicular bisector of BC.
Question 2.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A
AB = AC [Given]
AD = DA [Common]
BD = CD [Given]
∴ ∆ABD ≅ ∆ACD [By SSS congruency]
∠BAD = ∠CAD [By C.P.C.T.] …(1)
(ii) In ∆ABP and ∆ACP, we have
AB = AC [Given]
∠BAP = ∠CAP [From (1)]
∴ AP = PA [Common]
∴ ∆ABP ≅ ∆ACP [By SAS congruency]
(iii) Since, ∆ABP ≅ ∆ACP
⇒ ∠BAP = ∠CAP [By C.P.C.T.]
∴ AP is the bisector of ∠A.
Again, in ∆BDP and ∆CDP,
we have BD = CD [Given]
DP = PD [Common]
BP = CP [ ∵ ∆ABP ≅ ∆ACP]
⇒ A BDP = ACDP [By SSS congruency]
∴ ∠BDP = ∠CDP [By C.P.C.T.]
⇒ DP (or AP) is the bisector of ∠BDC
∴ AP is the bisector of ∠A as well as ∠D.
(iv) As, ∆ABP ≅ ∆ACP
⇒ ∠APS = ∠APC, BP = CP [By C.P.C.T.]
But ∠APB + ∠APC = 180° [Linear Pair]
∴ ∠APB = ∠APC = 90°
⇒ AP ⊥ BC, also BP = CP
Hence, AP is the perpendicular bisector of BC.
Question 2.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A
Solution:
(i) In right ∆ABD and ∆ACD, we have
AB =AC [Given]

∠ADB = ∠ADC [Each 90°]
AD = DA [Common]
∴ ∆ABD ≅ ∆ACD [By RHS congruency]
So, BD = CD [By C.P.C.T.]
⇒ D is the mid-point of BC or AD bisects BC.
(ii) Since, ∆ABD ≅ ∆ACD,
⇒ ∠BAD = ∠CAD [By C.P.C.T.]
So, AD bisects ∠A
Question 3.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and OR and median PN of ∆PQR (see figure). Show that
(i) ∆ABC ≅ ∆PQR
(ii) ∆ABM ≅ ∆PQN
AB =AC [Given]

∠ADB = ∠ADC [Each 90°]
AD = DA [Common]
∴ ∆ABD ≅ ∆ACD [By RHS congruency]
So, BD = CD [By C.P.C.T.]
⇒ D is the mid-point of BC or AD bisects BC.
(ii) Since, ∆ABD ≅ ∆ACD,
⇒ ∠BAD = ∠CAD [By C.P.C.T.]
So, AD bisects ∠A
Question 3.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and OR and median PN of ∆PQR (see figure). Show that
(i) ∆ABC ≅ ∆PQR
(ii) ∆ABM ≅ ∆PQN

Solution:
In ∆ABC, AM is the median.
∴BM = BC ……(1)
BC ……(1)
In ∆PQR, PN is the median.
∴ QN = QR …(2)
QR …(2)
And BC = QR [Given]
⇒ BC =
BC =  QR
QR
⇒ BM = QN …(3) [From (1) and (2)]
(i) In ∆ABM and ∆PQN, we have
AB = PQ , [Given]
AM = PN [Given]
BM = QN [From (3)]
∴ ∆ABM ≅ ∆PQN [By SSS congruency]
(ii) Since ∆ABM ≅ ∆PQN
⇒ ∠B = ∠Q …(4) [By C.P.C.T.]
Now, in ∆ABC and ∆PQR, we have
∠B = ∠Q [From (4)]
AB = PQ [Given]
BC = QR [Given]
∴ ∆ABC ≅ ∆PQR [By SAS congruency]
Question 4.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
In ∆ABC, AM is the median.
∴BM =
In ∆PQR, PN is the median.
∴ QN =
And BC = QR [Given]
⇒
⇒ BM = QN …(3) [From (1) and (2)]
(i) In ∆ABM and ∆PQN, we have
AB = PQ , [Given]
AM = PN [Given]
BM = QN [From (3)]
∴ ∆ABM ≅ ∆PQN [By SSS congruency]
(ii) Since ∆ABM ≅ ∆PQN
⇒ ∠B = ∠Q …(4) [By C.P.C.T.]
Now, in ∆ABC and ∆PQR, we have
∠B = ∠Q [From (4)]
AB = PQ [Given]
BC = QR [Given]
∴ ∆ABC ≅ ∆PQR [By SAS congruency]
Question 4.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:
Since BE ⊥ AC [Given]

∴ BEC is a right triangle such that ∠BEC = 90°
Similarly, ∠CFB = 90°
Now, in right ∆BEC and ∆CFB, we have
BE = CF [Given]
BC = CB [Common hypotenuse]
∠BEC = ∠CFB [Each 90°]
∴ ∆BEC ≅ ∆CFB [By RHS congruency]
So, ∠BCE = ∠CBF [By C.P.C.T.]
or ∠BCA = ∠CBA
Now, in ∆ABC, ∠BCA = ∠CBA
⇒ AB = AC [Sides opposite to equal angles of a ∆ are equal]
∴ ABC is an isosceles triangle.
Question 5.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Since BE ⊥ AC [Given]

∴ BEC is a right triangle such that ∠BEC = 90°
Similarly, ∠CFB = 90°
Now, in right ∆BEC and ∆CFB, we have
BE = CF [Given]
BC = CB [Common hypotenuse]
∠BEC = ∠CFB [Each 90°]
∴ ∆BEC ≅ ∆CFB [By RHS congruency]
So, ∠BCE = ∠CBF [By C.P.C.T.]
or ∠BCA = ∠CBA
Now, in ∆ABC, ∠BCA = ∠CBA
⇒ AB = AC [Sides opposite to equal angles of a ∆ are equal]
∴ ABC is an isosceles triangle.
Question 5.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution:
We have, AP ⊥ BC [Given]

∠APB = 90° and ∠APC = 90°
In ∆ABP and ∆ACP, we have
∠APB = ∠APC [Each 90°]
AB = AC [Given]
AP = AP [Common]
∴ ∆ABP ≅ ∆ACP [By RHS congruency]
So, ∠B = ∠C [By C.P.C.T.]

∠APB = 90° and ∠APC = 90°
In ∆ABP and ∆ACP, we have
∠APB = ∠APC [Each 90°]
AB = AC [Given]
AP = AP [Common]
∴ ∆ABP ≅ ∆ACP [By RHS congruency]
So, ∠B = ∠C [By C.P.C.T.]
Exercise 7.4
Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.
Show that in a right angled triangle, the hypotenuse is the longest side.
Solution:
Let us consider ∆ABC such that ∠B = 90°
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 90°-+ ∠C = 180°
⇒ ∠A + ∠C = 90°
⇒∠A + ∠C = ∠B
∴ ∠B > ∠A and ∠B > ∠C

⇒ Side opposite to ∠B is longer than the side opposite to ∠A
i.e., AC > BC.
Similarly, AC > AB.
Therefore, we get AC is the longest side. But AC is the hypotenuse of the triangle. Thus, the hypotenuse is the longest side.
Question 2.
In figure, sides AB and AC of ∆ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 90°-+ ∠C = 180°
⇒ ∠A + ∠C = 90°
⇒∠A + ∠C = ∠B
∴ ∠B > ∠A and ∠B > ∠C

⇒ Side opposite to ∠B is longer than the side opposite to ∠A
i.e., AC > BC.
Similarly, AC > AB.
Therefore, we get AC is the longest side. But AC is the hypotenuse of the triangle. Thus, the hypotenuse is the longest side.
Question 2.
In figure, sides AB and AC of ∆ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

Solution:
∠ABC + ∠PBC = 180° [Linear pair]
and ∠ACB + ∠QCB = 180° [Linear pair]
But ∠PBC < ∠QCB [Given] ⇒ 180° – ∠PBC > 180° – ∠QCB
⇒ ∠ABC > ∠ACB
The side opposite to ∠ABC > the side opposite to ∠ACB
⇒ AC > AB.
Question 3.
In figure, ∠B <∠ A and ∠C <∠ D. Show that AD < BC.
∠ABC + ∠PBC = 180° [Linear pair]
and ∠ACB + ∠QCB = 180° [Linear pair]
But ∠PBC < ∠QCB [Given] ⇒ 180° – ∠PBC > 180° – ∠QCB
⇒ ∠ABC > ∠ACB
The side opposite to ∠ABC > the side opposite to ∠ACB
⇒ AC > AB.
Question 3.
In figure, ∠B <∠ A and ∠C <∠ D. Show that AD < BC.

Solution: Since ∠A > ∠B [Given]
∴ OB > OA …(1)
[Side opposite to greater angle is longer]
Similarly, OC > OD …(2)
Adding (1) and (2), we have
OB + OC > OA + OD
⇒ BC > AD
Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠ A > ∠C and ∠B >∠D.
∴ OB > OA …(1)
[Side opposite to greater angle is longer]
Similarly, OC > OD …(2)
Adding (1) and (2), we have
OB + OC > OA + OD
⇒ BC > AD
Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠ A > ∠C and ∠B >∠D.

Solution:
Let us join AC.

Now, in ∆ABC, AB < BC [∵ AB is the smallest side of the quadrilateral ABCD] ⇒ BC > AB
⇒ ∠BAC > ∠BCA …(1)
[Angle opposite to longer side of A is greater]
Again, in ∆ACD, CD > AD
[ CD is the longest side of the quadrilateral ABCD]
⇒ ∠CAD > ∠ACD …(2)
[Angle opposite to longer side of ∆ is greater]
Adding (1) and (2), we get
∠BAC + ∠CAD > ∠BCA + ∠ACD
⇒ ∠A > ∠C
Similarly, by joining BD, we have ∠B > ∠D.
Question 5.
In figure, PR > PQ and PS bisect ∠QPR. Prove that ∠PSR >∠PSQ.

Now, in ∆ABC, AB < BC [∵ AB is the smallest side of the quadrilateral ABCD] ⇒ BC > AB
⇒ ∠BAC > ∠BCA …(1)
[Angle opposite to longer side of A is greater]
Again, in ∆ACD, CD > AD
[ CD is the longest side of the quadrilateral ABCD]
⇒ ∠CAD > ∠ACD …(2)
[Angle opposite to longer side of ∆ is greater]
Adding (1) and (2), we get
∠BAC + ∠CAD > ∠BCA + ∠ACD
⇒ ∠A > ∠C
Similarly, by joining BD, we have ∠B > ∠D.
Question 5.
In figure, PR > PQ and PS bisect ∠QPR. Prove that ∠PSR >∠PSQ.

Solution:
In ∆PQR, PS bisects ∠QPR [Given]
∴ ∠QPS = ∠RPS
and PR > PQ [Given]
⇒ ∠PQS > ∠PRS [Angle opposite to longer side of A is greater]
⇒ ∠PQS + ∠QPS > ∠PRS + ∠RPS …(1) [∵∠QPS = ∠RPS]
∵ Exterior ∠PSR = [∠PQS + ∠QPS]
and exterior ∠PSQ = [∠PRS + ∠RPS]
[An exterior angle is equal to the sum of interior opposite angles]
Now, from (1), we have
∠PSR = ∠PSQ.
Question 6.
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
∴ ∠QPS = ∠RPS
and PR > PQ [Given]
⇒ ∠PQS > ∠PRS [Angle opposite to longer side of A is greater]
⇒ ∠PQS + ∠QPS > ∠PRS + ∠RPS …(1) [∵∠QPS = ∠RPS]
∵ Exterior ∠PSR = [∠PQS + ∠QPS]
and exterior ∠PSQ = [∠PRS + ∠RPS]
[An exterior angle is equal to the sum of interior opposite angles]
Now, from (1), we have
∠PSR = ∠PSQ.
Question 6.
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Solution:
Let us consider the ∆PMN such that ∠M = 90°

Since, ∠M + ∠N+ ∠P = 180°
[Sum of angles of a triangle is 180°]
∵ ∠M = 90° [PM ⊥ l]
So, ∠N + ∠P = ∠M
⇒ ∠N < ∠M
⇒ PM < PN …(1)
Similarly, PM < PN1 …(2)
and PM < PN2 …(3)
From (1), (2) and (3), we have PM is the smallest line segment drawn from P on the line l. Thus, the perpendicular line segment is the shortest line segment drawn on a line from a point not on it.
Exercise 7.5
Let us consider the ∆PMN such that ∠M = 90°

Since, ∠M + ∠N+ ∠P = 180°
[Sum of angles of a triangle is 180°]
∵ ∠M = 90° [PM ⊥ l]
So, ∠N + ∠P = ∠M
⇒ ∠N < ∠M
⇒ PM < PN …(1)
Similarly, PM < PN1 …(2)
and PM < PN2 …(3)
From (1), (2) and (3), we have PM is the smallest line segment drawn from P on the line l. Thus, the perpendicular line segment is the shortest line segment drawn on a line from a point not on it.
Exercise 7.5
Question 1.
ABC is a triangle. Locate a point in the interior of ∆ ABC which is equidistant from all the vertices of ∆ ABC.
ABC is a triangle. Locate a point in the interior of ∆ ABC which is equidistant from all the vertices of ∆ ABC.
Solution:
Let us consider a ∆ABC.
Draw l, the perpendicular bisector of AB.
Draw m, the perpendicular bisector of BC.
Let the two perpendicular bisectors l and m meet at O.
O is the required point which is equidistant from A, B and C.

Note: If we draw a circle with centre O and radius OB or OC, then it will pass through A, B and C. The point O is called circumcentre of the triangle.
Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Let us consider a ∆ABC.
Draw l, the perpendicular bisector of AB.
Draw m, the perpendicular bisector of BC.
Let the two perpendicular bisectors l and m meet at O.
O is the required point which is equidistant from A, B and C.

Note: If we draw a circle with centre O and radius OB or OC, then it will pass through A, B and C. The point O is called circumcentre of the triangle.
Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Solution:
Let us consider a ∆ABC.

Draw m, the bisector of ∠C.
Let the two bisectors l and m meet at O.
Thus, O is the required point which is equidistant from the sides of ∆ABC.
Note: If we draw OM ⊥ BC and draw a circle with O as centre and OM as radius, then the circle will touch the sides of the triangle. Point O is called incentre of the triangle.

Question 3.
In a huge park, people are concentrated at three points (see figure)
A: where these are different slides and swings for children.
B: near which a man-made lake is situated.
C: which is near to a large parking and exist.
Where should an ice-cream parlor be set? up so that maximum number of persons can approach it?
[Hint The parlour should be equidistant from A, B and C.]
Let us consider a ∆ABC.

Draw m, the bisector of ∠C.
Let the two bisectors l and m meet at O.
Thus, O is the required point which is equidistant from the sides of ∆ABC.
Note: If we draw OM ⊥ BC and draw a circle with O as centre and OM as radius, then the circle will touch the sides of the triangle. Point O is called incentre of the triangle.

Question 3.
In a huge park, people are concentrated at three points (see figure)

A: where these are different slides and swings for children.
B: near which a man-made lake is situated.
C: which is near to a large parking and exist.
Where should an ice-cream parlor be set? up so that maximum number of persons can approach it?
[Hint The parlour should be equidistant from A, B and C.]
Solution:
Let us join A and B, and draw l, the perpendicular bisector of AB.
Now, join B and C, and draw m, the perpendicular bisector of BC. Let the perpendicular bisectors l and m meet at O.
The point O is the required point where the ice cream parlour be set up.
Note: If we join A and C and draw the perpendicular bisector, then it will also meet (or pass through) the point O.

Question 4.
Complete the hexagonal and star shaped Rangolies [see Fig. (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
Let us join A and B, and draw l, the perpendicular bisector of AB.
Now, join B and C, and draw m, the perpendicular bisector of BC. Let the perpendicular bisectors l and m meet at O.
The point O is the required point where the ice cream parlour be set up.
Note: If we join A and C and draw the perpendicular bisector, then it will also meet (or pass through) the point O.

Question 4.
Complete the hexagonal and star shaped Rangolies [see Fig. (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

Solution:
It is an activity.
We require 150 equilateral triangles of side 1 cm in the Fig. (i) and 300 equilateral triangles in the Fig. (ii).
∴ The Fig. (ii) has more triangles.
It is an activity.
We require 150 equilateral triangles of side 1 cm in the Fig. (i) and 300 equilateral triangles in the Fig. (ii).
∴ The Fig. (ii) has more triangles.